what does it mean to be in the 5th percentile

Statistic which divides a information fix into 100 parts and analyzes it equally a percentage

In statistics, a k-th percentile (percentile score or centile) is a score below which a given percentage k of scores in its frequency distribution falls (sectional definition) or a score at or beneath which a given per centum falls (inclusive definition). For example, the 50th percentile (the median) is the score below which (exclusive) or at or below which (inclusive) 50% of the scores in the distribution may be plant. Percentiles are expressed in the same unit of measurement as the input scores; for example, if the scores refer to human weight, the corresponding percentiles will exist expressed in kilograms or pounds.

The percentile score and the percentile rank are related terms. The percentile rank of a score is the percentage of scores in its distribution that are less than it, an exclusive definition, and one that tin exist expressed with a single, simple formula. Percentile scores and percentile ranks are ofttimes used in the reporting of test scores from norm-referenced tests, simply, as simply noted, they are non the same. For percentile rank, a score is given and a percentage is computed. Percentile ranks are exclusive. If the percentile rank for a specified score is 90%, then 90% of the scores were lower. In contrast, for percentiles a percentage is given and a corresponding score is determined, which can exist either exclusive or inclusive. The score for a specified per centum (east.thousand., 90th) indicates a score beneath which (sectional definition) or at or below which (inclusive definition) other scores in the distribution fall.

The 25th percentile is also known as the first quartile (Q _one), the 50th percentile as the median or 2nd quartile (Q _two), and the 75th percentile equally the third quartile (Q _three).

Applications [edit]

When ISPs bill "burstable" internet bandwidth, the 95th or 98th percentile commonly cuts off the height 5% or 2% of bandwidth peaks in each month, and so bills at the nearest rate. In this way, infrequent peaks are ignored, and the customer is charged in a fairer way. The reason this statistic is and so useful in measuring data throughput is that information technology gives a very accurate picture of the price of the bandwidth. The 95th percentile says that 95% of the fourth dimension, the usage is below this amount: so, the remaining 5% of the time, the usage is higher up that corporeality.

Physicians will ofttimes utilize infant and children'southward weight and height to assess their growth in comparison to national averages and percentiles which are found in growth charts.

The 85th percentile speed of traffic on a road is oftentimes used as a guideline in setting speed limits and assessing whether such a limit is besides loftier or low.^{[1] [ii]}

In finance, value at gamble is a standard measure to assess (in a model-dependent fashion) the quantity under which the value of the portfolio is not expected to sink inside a given period of time and given a confidence value.

The normal distribution and percentiles [edit]

Representation of the iii-sigma rule. The dark blue zone represents observations within ane standard deviation (σ) to either side of the mean (μ), which accounts for about 68.3% of the population. Two standard deviations from the mean (dark and medium blue) account for about 95.4%, and 3 standard deviations (dark, medium, and light blue) for nearly 99.seven%.

The methods given in the definitions section (below) are approximations for use in small-sample statistics. In general terms, for very big populations following a normal distribution, percentiles may often be represented by reference to a normal curve plot. The normal distribution is plotted along an axis scaled to standard deviations, or sigma ( ${\displaystyle \sigma }$ ) units. Mathematically, the normal distribution extends to negative infinity on the left and positive infinity on the correct. Annotation, still, that only a very minor proportion of individuals in a population will fall exterior the −3σ to +3σ range. For example, with human heights very few people are higher up the +3σ height level.

Percentiles represent the area under the normal curve, increasing from left to right. Each standard deviation represents a fixed percentile. Thus, rounding to ii decimal places, −3σ is the 0.13th percentile, −2σ the 2.28th percentile, −1σ the xv.87th percentile, 0σ the 50th percentile (both the hateful and median of the distribution), +oneσ the 84.13th percentile, +2σ the 97.72nd percentile, and +3σ the 99.87th percentile. This is related to the 68–95–99.7 rule or the three-sigma rule. Notation that in theory the 0th percentile falls at negative infinity and the 100th percentile at positive infinity, although in many practical applications, such as test results, natural lower and/or upper limits are enforced.

Definitions [edit]

There is no standard definition of percentile,^{[3] [4] [5]} yet all definitions yield similar results when the number of observations is very big and the probability distribution is continuous.^[6] In the limit, as the sample size approaches infinity, the 100p ^th percentile (0<p<1) approximates the inverse of the cumulative distribution part (CDF) thus formed, evaluated at p, every bit p approximates the CDF. This can be seen as a outcome of the Glivenko–Cantelli theorem. Some methods for calculating the percentiles are given below.

Adding methods [edit]

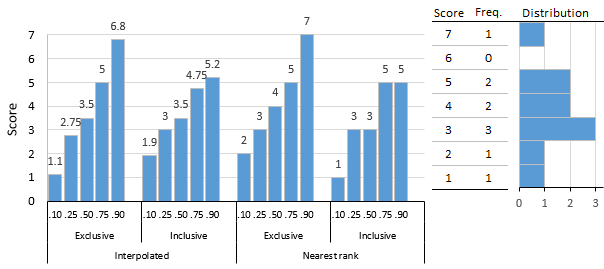
Interpolated and nearest-rank, exclusive and inclusive, percentiles for 10-score distribution.

There are many formulas or algorithms^[7] for a percentile score. Hyndman and Fan ^[3] identified ix and most statistical and spreadsheet software use 1 of the methods they depict.^[viii] Algorithms either render the value of a score that exists in the gear up of scores (nearest-rank methods) or interpolate between existing scores and are either exclusive or inclusive.

Nearest-rank methods (sectional/inclusive)

PC: percentile specified	0.x	0.25	0.50	0.75	0.xc
N: Number of scores	10	10	10	10	10
OR: ordinal rank = PC × N	i	2.5	5	7.5	9
Rank: >OR / ≥OR	2/i	three/3	half-dozen/5	8/viii	ten/9
Score at rank (exc/inc)	2/ane	3/3	4/3	5/5	seven/5

The figure shows a 10-score distribution, illustrates the percentile scores that effect from these different algorithms, and serves as an introduction to the examples given afterwards. The simplest are nearest-rank methods that return a score from the distribution, although compared to interpolation methods, results can exist a bit crude. The Nearest-Rank Methods tabular array shows the computational steps for exclusive and inclusive methods.

Interpolated methods (exclusive/inclusive)

PC: percentile specified	0.x	0.25	0.50	0.75	0.90
N: number of scores	x	10	ten	10	10
OR: PC×(N+1) / PC×(N−1)+1	ane.1/1.9	ii.75/3.25	5.5/5.v	eight.25/7.75	9.9/9.1
LoRank: OR truncated	1/i	ii/iii	5/5	eight/7	ix/9
HIRank: OR rounded upwardly	ii/2	3/4	6/half-dozen	9/8	ten/10
LoScore: score at LoRank	ane/ane	2/3	3/3	v/4	v/5
HiScore: score at HiRank	2/two	iii/iii	4/4	5/v	7/vii
Difference: HiScore − LoScore	i/1	1/0	1/1	0/1	2/two
Modernistic: fractional office of OR	0.ane/0.9	0.75/0.25	0.5/0.5	0.25/0.75	0.9/0.1
Interpolated score (exc/inc) = LoScore + Mod × Difference	1.1/1.9	2.75/3	3.5/3.five	five/4.75	six.8/5.two

Interpolation methods, as the name implies, can return a score that is between scores in the distribution. Algorithms used by statistical programs typically employ interpolation methods, for example, the percentile.exc and percentile.inc functions in Microsoft Excel. The Interpolated Methods table shows the computational steps.

The nearest-rank method [edit]

The percentile values for the ordered list {xv, twenty, 35, twoscore, 50}

One definition of percentile, often given in texts, is that the P-th percentile ${\displaystyle (0<P\leq 100)}$ of a list of Due north ordered values (sorted from least to greatest) is the smallest value in the listing such that no more than P pct of the data is strictly less than the value and at least P per centum of the data is less than or equal to that value. This is obtained by first calculating the ordinal rank so taking the value from the ordered listing that corresponds to that rank. The ordinal rank n is calculated using this formula

${\displaystyle n=\left\lceil {\frac {P}{100}}\times North\correct\rceil .}$

Note the following:

• Using the nearest-rank method on lists with fewer than 100 distinct values can effect in the aforementioned value being used for more than one percentile.
• A percentile calculated using the nearest-rank method will e'er be a fellow member of the original ordered list.
• The 100th percentile is defined to be the largest value in the ordered list.

Worked examples of the nearest-rank method [edit]

Example one

Consider the ordered list {15, 20, 35, 40, 50}, which contains 5 data values. What are the fifth, 30th, 40th, 50th and 100th percentiles of this list using the nearest-rank method?

Percentile P	Number in list N	Ordinal rank n	Number from the ordered list that has that rank	Percentile value	Notes
5th	5	${\displaystyle \left\lceil {\frac {five}{100}}\times 5\right\rceil =\lceil 0.25\rceil =1}$	the first number in the ordered list, which is xv	15	15 is the smallest element of the list; 0% of the data is strictly less than 15, and xx% of the data is less than or equal to 15.
30th	five	${\displaystyle \left\lceil {\frac {xxx}{100}}\times five\right\rceil =\lceil 1.five\rceil =2}$	the 2nd number in the ordered list, which is 20	20	20 is an element of the ordered list.
40th	5	${\displaystyle \left\lceil {\frac {40}{100}}\times 5\right\rceil =\lceil 2.0\rceil =2}$	the second number in the ordered listing, which is xx	20	In this example, information technology is the aforementioned every bit the 30th percentile.
50th	5	${\displaystyle \left\lceil {\frac {50}{100}}\times v\correct\rceil =\lceil ii.five\rceil =3}$	the tertiary number in the ordered list, which is 35	35	35 is an element of the ordered listing.
100th	5	${\displaystyle \left\lceil {\frac {100}{100}}\times 5\right\rceil =\lceil 5\rceil =5}$	the terminal number in the ordered list, which is 50	50	The 100th percentile is divers to exist the largest value in the listing, which is 50.

And so the 5th, 30th, 40th, 50th and 100th percentiles of the ordered list {15, 20, 35, twoscore, 50} using the nearest-rank method are {15, 20, twenty, 35, fifty}.

Example 2

Consider an ordered population of x information values {3, six, 7, 8, 8, 10, 13, fifteen, 16, 20}. What are the 25th, 50th, 75th and 100th percentiles of this list using the nearest-rank method?

Percentile P	Number in list N	Ordinal rank northward	Number from the ordered list that has that rank	Percentile value	Notes
25th	10	${\displaystyle \left\lceil {\frac {25}{100}}\times 10\right\rceil =\lceil 2.5\rceil =3}$	the 3rd number in the ordered listing, which is vii	seven	7 is an element of the list.
50th	10	${\displaystyle \left\lceil {\frac {50}{100}}\times 10\right\rceil =\lceil 5.0\rceil =five}$	the 5th number in the ordered list, which is viii	8	8 is an element of the listing.
75th	x	${\displaystyle \left\lceil {\frac {75}{100}}\times 10\right\rceil =\lceil 7.v\rceil =8}$	the 8th number in the ordered listing, which is 15	15	15 is an element of the list.
100th	10	Concluding	xx, which is the final number in the ordered listing	twenty	The 100th percentile is defined to be the largest value in the list, which is 20.

So the 25th, 50th, 75th and 100th percentiles of the ordered list {3, 6, vii, 8, 8, 10, thirteen, 15, 16, 20} using the nearest-rank method are {vii, 8, 15, 20}.

Case 3

Consider an ordered population of xi data values {3, 6, 7, 8, 8, 9, 10, 13, 15, xvi, twenty}. What are the 25th, 50th, 75th and 100th percentiles of this listing using the nearest-rank method?

Percentile P	Number in listing N	Ordinal rank n	Number from the ordered list that has that rank	Percentile value	Notes
25th	xi	${\displaystyle \left\lceil {\frac {25}{100}}\times 11\right\rceil =\lceil 2.75\rceil =3}$	the third number in the ordered listing, which is 7	7	7 is an element of the list.
50th	eleven	${\displaystyle \left\lceil {\frac {50}{100}}\times 11\right\rceil =\lceil v.fifty\rceil =6}$	the 6th number in the ordered listing, which is 9	nine	9 is an element of the list.
75th	11	${\displaystyle \left\lceil {\frac {75}{100}}\times 11\right\rceil =\lceil 8.25\rceil =9}$	the 9th number in the ordered list, which is 15	15	15 is an element of the list.
100th	11	Final	20, which is the terminal number in the ordered list	twenty	The 100th percentile is defined to exist the largest value in the list, which is xx.

So the 25th, 50th, 75th and 100th percentiles of the ordered list {three, vi, 7, 8, 8, 9, 10, 13, 15, 16, twenty} using the nearest-rank method are {7, nine, xv, 20}.

The linear interpolation betwixt closest ranks method [edit]

An alternative to rounding used in many applications is to use linear interpolation between adjacent ranks.

Commonalities between the variants of this method [edit]

All of the post-obit variants accept the following in mutual. Given the order statistics

${\displaystyle \{v_{i},i=1,ii,\ldots ,N:v_{i+1}\geq v_{i},\forall i=1,2,\ldots ,North-i\},}$

we seek a linear interpolation office that passes through the points ${\displaystyle (v_{i},i)}$ . This is simply accomplished by

${\displaystyle five(10)=v_{\lfloor x\rfloor }+(x{\bmod {1}})(v_{\lfloor x\rfloor +ane}-v_{\lfloor x\rfloor }),\forall x\in [1,N]:v(i)=v_{i}{\text{, for }}i=i,ii,\ldots ,N,}$

where ${\displaystyle \lfloor 10\rfloor }$ uses the floor function to represent the integral part of positive ten, whereas ${\displaystyle 10{\bmod {1}}}$ uses the modernistic function to represent its fractional role (the remainder after sectionalisation past 1). (Notation that, though at the endpoint ${\displaystyle x=Northward}$ , ${\displaystyle v_{\lfloor x\rfloor +1}}$ is undefined, it does non need to be considering it is multiplied by ${\displaystyle x{\bmod {ane}}=0}$ .) As we can see, x is the continuous version of the subscript i, linearly interpolating v between next nodes.

There are two ways in which the variant approaches differ. The first is in the linear human relationship betwixt the rank x, the percent rank ${\displaystyle P=100p}$ , and a constant that is a function of the sample size N:

${\displaystyle 10=f(p,N)=(N+c_{1})p+c_{2}.}$

In that location is the additional requirement that the midpoint of the range ${\displaystyle (1,N)}$ , corresponding to the median, occur at ${\displaystyle p=0.5}$ :

${\displaystyle {\brainstorm{aligned}f(0.5,N)&={\frac {Northward+c_{1}}{2}}+c_{ii}={\frac {N+1}{2}}\\\therefore 2c_{2}+c_{1}&=1\end{aligned}},}$

and our revised function now has simply one caste of freedom, looking like this:

${\displaystyle ten=f(p,Due north)=(N+i-2C)p+C.}$

The second mode in which the variants differ is in the definition of the office well-nigh the margins of the ${\displaystyle [0,1]}$ range of p: ${\displaystyle f(p,North)}$ should produce, or exist forced to produce, a result in the range ${\displaystyle [ane,North]}$ , which may mean the absence of a one-to-one correspondence in the wider region. One author has suggested a selection of ${\displaystyle C={\tfrac {one}{2}}(1+\xi )}$ where ξ is the shape of the Generalized extreme value distribution which is the farthermost value limit of the sampled distribution.

First variant, C = 1/2 [edit]

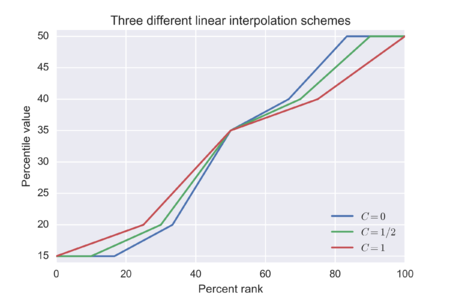
The result of using each of the three variants on the ordered list {xv, 20, 35, 40, 50}

(Sources: Matlab "prctile" function,^{[9] [10]})

${\displaystyle x=f(p)={\brainstorm{cases}Np+{\frac {ane}{2}},\forall p\in \left[p_{i},p_{N}\right],\\1,\forall p\in \left[0,p_{1}\right],\\N,\forall p\in \left[p_{Due north},ane\correct].\end{cases}}}$

where

${\displaystyle p_{i}={\frac {1}{N}}\left(i-{\frac {1}{ii}}\right),i\in [one,N]\cap \mathbb {N} }$

${\displaystyle \therefore p_{1}={\frac {ane}{2N}},p_{N}={\frac {2N-1}{2N}}.}$

Furthermore, permit

${\displaystyle P_{i}=100p_{i}.}$

The inverse relationship is restricted to a narrower region:

${\displaystyle p={\frac {1}{N}}\left(10-{\frac {1}{2}}\right),x\in (i,N)\cap \mathbb {R} .}$

Worked example of the showtime variant [edit]

Consider the ordered list {15, 20, 35, twoscore, l}, which contains five data values. What are the 5th, 30th, 40th and 95th percentiles of this list using the Linear Interpolation Between Closest Ranks method? First, we calculate the percent rank for each list value.

Listing value ${\displaystyle v_{i}}$	Position of that value in the ordered listing i	Number of values Due north	Calculation of percent rank	Percent rank, ${\displaystyle P_{i}}$
xv	i	5	${\displaystyle {\frac {100}{5}}\left(1-{\frac {1}{2}}\right)=10.}$	10
20	2	five	${\displaystyle {\frac {100}{5}}\left(2-{\frac {1}{2}}\correct)=xxx.}$	30
35	3	5	${\displaystyle {\frac {100}{v}}\left(three-{\frac {1}{ii}}\right)=50.}$	50
xl	four	5	${\displaystyle {\frac {100}{5}}\left(4-{\frac {1}{2}}\correct)=70.}$	seventy
fifty	5	5	${\displaystyle {\frac {100}{5}}\left(5-{\frac {one}{2}}\correct)=90.}$	ninety

Then we take those pct ranks and calculate the percentile values equally follows:

Percent rank P	Number of values N	Is ${\displaystyle P<P_{ane}}$ ?	Is ${\displaystyle P>P_{n}}$ ?	Is there a percent rank equal to P?	What do we utilize for percentile value?	Percentile value ${\displaystyle v(f(p))}$	Notes
5	5	Aye	No	No	We see that ${\displaystyle P=5}$ , which is less than the first percent rank ${\displaystyle p_{1}=10}$ , and so apply the beginning list value ${\displaystyle v_{1}}$ , which is fifteen	15	15 is a member of the ordered list
thirty	v	No	No	Yes	We encounter that ${\displaystyle P=30}$ is the same as the 2nd percent rank ${\displaystyle p_{2}=30}$ , so use the second list value ${\displaystyle v_{two}}$ , which is 20	xx	20 is a member of the ordered listing
forty	v	No	No	No	We see that ${\displaystyle P=40}$ is between pct rank ${\displaystyle p_{two}=xxx}$ and ${\displaystyle p_{3}=50}$ , so we take ${\displaystyle k=ii,k+1=3,P=xl,p_{k}=p_{two}=xxx,v_{k}=v_{two}=20,v_{thousand+1}=v_{iii}=35,N=5}$ . Given those values we tin can then calculate v equally follows: ${\displaystyle v=20+5\times {\frac {xl-xxx}{100}}(35-xx)=27.5}$	27.5	27.5 is not a member of the ordered list
95	5	No	Yes	No	Nosotros come across that ${\displaystyle P=95}$ , which is greater than the final percent rank ${\displaystyle p_{Due north}=ninety}$ , then utilize the last list value, which is 50	50	50 is a fellow member of the ordered list

So the 5th, 30th, 40th and 95th percentiles of the ordered list {fifteen, twenty, 35, 40, 50} using the Linear Interpolation Between Closest Ranks method are {fifteen, 20, 27.5, 50}

Second variant, C = one [edit]

(Source: Some software packages, including NumPy^[11] and Microsoft Excel^[5] (up to and including version 2013 by means of the PERCENTILE.INC function). Noted every bit an culling by NIST^[8])

${\displaystyle x=f(p,North)=p(N-1)+1{\text{, }}p\in [0,1]}$

${\displaystyle \therefore p={\frac {ten-1}{N-one}}{\text{, }}x\in [1,North].}$

Note that the ${\displaystyle x\leftrightarrow p}$ relationship is ane-to-ane for ${\displaystyle p\in [0,i]}$ , the merely ane of the three variants with this property; hence the "INC" suffix, for inclusive, on the Excel part.

Worked examples of the second variant [edit]

Example 1 [edit]

Consider the ordered listing {xv, 20, 35, 40, 50}, which contains v data values. What is the 40th percentile of this list using this variant method?

First we summate the rank of the 40th percentile:

${\displaystyle ten={\frac {forty}{100}}(5-1)+1=2.6}$

And then, x=2.6, which gives us ${\displaystyle \lfloor 10\rfloor =2}$ and ${\displaystyle ten{\bmod {1}}=0.half-dozen}$ . So, the value of the 40th percentile is

${\displaystyle 5(2.6)=v_{2}+0.six(v_{3}-v_{2})=20+0.6(35-20)=29.}$

Case 2 [edit]

Consider the ordered list {1,2,three,4} which contains four information values. What is the 75th percentile of this list using the Microsoft Excel method?

First we calculate the rank of the 75th percentile every bit follows:

${\displaystyle x={\frac {75}{100}}(4-one)+1=three.25}$

So, x=three.25, which gives united states of america an integral part of 3 and a fractional role of 0.25. And so, the value of the 75th percentile is

${\displaystyle v(3.25)=v_{3}+0.25(v_{four}-v_{3})=3+0.25(4-3)=3.25.}$

Tertiary variant, C = 0 [edit]

(The principal variant recommended by NIST.^[eight] Adopted past Microsoft Excel since 2010 by means of PERCENTIL.EXC function. However, as the "EXC" suffix indicates, the Excel version excludes both endpoints of the range of p, i.eastward., ${\displaystyle p\in (0,one)}$ , whereas the "INC" version, the second variant, does non; in fact, whatsoever number smaller than ${\displaystyle {\frac {1}{Northward+i}}}$ is also excluded and would cause an mistake.)

${\displaystyle ten=f(p,Northward)={\begin{cases}one{\text{, }}p\in \left[0,{\frac {1}{North+1}}\right]\\p(Due north+1){\text{, }}p\in \left({\frac {1}{N+1}},{\frac {N}{N+1}}\right)\\N{\text{, }}p\in \left[{\frac {N}{Northward+ane}},1\right]\end{cases}}.}$

The inverse is restricted to a narrower region:

${\displaystyle p={\frac {x}{N+1}}{\text{, }}10\in (0,Northward).}$

Worked case of the third variant [edit]

Consider the ordered list {15, xx, 35, 40, 50}, which contains v data values. What is the 40th percentile of this list using the NIST method?

Commencement we calculate the rank of the 40th percentile every bit follows:

${\displaystyle ten={\frac {40}{100}}(5+one)=2.4}$

So x=2.4, which gives u.s. ${\displaystyle \lfloor 10\rfloor =ii}$ and ${\displaystyle x{\bmod {1}}=0.4}$ . And so the value of the 40th percentile is calculated as:

${\displaystyle v(2.4)=v_{2}+0.iv(v_{3}-v_{2})=20+0.4(35-20)=26}$

So the value of the 40th percentile of the ordered list {15, xx, 35, xl, l} using this variant method is 26.

The weighted percentile method [edit]

In add-on to the percentile function, there is too a weighted percentile, where the pct in the full weight is counted instead of the total number. At that place is no standard office for a weighted percentile. 1 method extends the higher up approach in a natural way.

Suppose we accept positive weights ${\displaystyle w_{1},w_{2},w_{3},\dots ,w_{Due north}}$ associated, respectively, with our North sorted sample values. Let

${\displaystyle S_{N}=\sum _{thousand=1}^{N}w_{thousand},}$

the sum of the weights. And then the formulas above are generalized by taking

${\displaystyle p_{n}={\frac {1}{S_{N}}}\left(S_{due north}-{\frac {w_{n}}{ii}}\right)}$ when ${\displaystyle C=1/two}$ ,

or

${\displaystyle p_{n}={\frac {S_{n}-Cw_{n}}{S_{N}+(i-2C)w_{north}}}}$ for general ${\displaystyle C}$ ,

and

${\displaystyle v=v_{k}+{\frac {P-p_{k}}{p_{thousand+1}-p_{one thousand}}}(v_{grand+1}-v_{k}).}$

The 50% weighted percentile is known every bit the weighted median.

Come across also [edit]

• Quantile
• Decile
• Summary statistics
• Percentile rank

References [edit]

1. ^ Johnson, Robert; Kuby, Patricia (2007), "Applied Example 2.fifteen, The 85th Percentile Speed Limit: Going With 85% of the Flow", Unproblematic Statistics (tenth ed.), Cengage Learning, p. 102, ISBN9781111802493 .
2. ^ "Rational Speed Limits and the 85th Percentile Speed" (PDF). lsp.org. Louisiana State Police force. Archived from the original (PDF) on 23 September 2018. Retrieved 28 Oct 2018.
3. ^ ^{a b} Hyndman, Rob J.; Fan, Yanan (Nov 1996). "Sample Quantiles in Statistical Packages". American Statistician. American Statistical Clan. 50 (four): 361–365. doi:ten.2307/2684934. JSTOR 2684934.
4. ^ Lane, David. "Percentiles". Retrieved 2007-09-15 .
5. ^ ^{a b} Pottel, Hans. "Statistical flaws in Excel" (PDF). Archived from the original (PDF) on 2013-06-04. Retrieved 2013-03-25 .
6. ^ Schoonjans F, De Bacquer D, Schmid P (2011). "Estimation of population percentiles". Epidemiology. 22 (5): 750–751. doi:10.1097/EDE.0b013e318225c1de. PMC3171208. PMID 21811118.
7. ^ Wessa, P (2021). "Percentiles in Free Statistics Software". Office for Research Development and Education. Retrieved 13 Nov 2021.
8. ^ ^{a b c} "Engineering Statistics Handbook: Percentile". NIST. Retrieved 2009-02-18 .
9. ^ "Matlab Statistics Toolbox – Percentiles". Retrieved 2006-09-fifteen . , This is equivalent to Method v discussed here
10. ^ Langford, E. (2006). "Quartiles in Elementary Statistics". Journal of Statistics Instruction. 14 (three). doi:ten.1080/10691898.2006.11910589.
11. ^ "NumPy i.12 documentation". SciPy. Retrieved 2017-03-xix .

knightprodins.blogspot.com

Source: https://en.wikipedia.org/wiki/Percentile